前: 変換モジュール 次: プロバティウインドウ
7. パターンモジュール
「パターン」カテゴリのモジュールは手続きテクスチャの作成に便利なさまざまなパターンを提供します。
空間中の点の X, Y, (場合によって)Z 座標に対応する入力と、その点にパターンを与える出力が1つかそれ以上あります。
ノイズ
Ken Perlin の勾配ノイズ関数のオクターブをいくつも足し合わせて、フラクタルノイズパターンを作成します。各オクターブはその前のオクターブの周期を2倍にします。オクターブ数と最初のオクターブの振幅は指定できます。高いほうのオクターブそれぞれの振幅は、その前のオクターブの振幅を ノイズ 入力ポート(典型的には0〜1ですが、必ずというわけではありません)で乗算して求められます。これはパラメータではなく入力ポートなので、定数である必要はありません。このモジュールは、キャラクターの表面にわたって異なるノイズパターンを作るのにとても便利です。
ノイズ関数は、出力値が典型的には0〜1となるよう拡大縮小されます。しかしパラメータの値とノイズ入力により、出力値はこの範囲を超えることがあります。

乱流
ノイズの各オクターブを足し合わせる前にその絶対値を取ること以外は、ノイズモジュールに似ています。これで誘導された不連続な変化で、「しわ」を作って出力します。結果は液体の乱流を思わせるものになります。
ノイズ関数は、出力値が典型的には0〜1となるよう拡大縮小されます。しかしパラメータの値とノイズ入力により、出力値は1を超えることがあります。
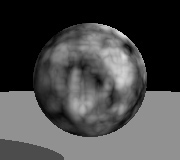
網目
一様な網目をもとにしたパターンを作成するのに便利です。これは一様で3次元の「特徴点」の格子を定義します。空間上で1つの点を与えると、このモジュールはその点とその点に最も近い特徴点の間の距離を出力します。特徴点との間隔を変えるには、モジュールをダブルクリックします。

細胞
Steven Worley の細胞テクスチャ基準関数(Cellular Texture Basis Function)を提供します。上述の網目関数と似ていますが、特徴点が空間中にランダムに散っていて、網目のように並んではいない点が異なります。
出力ポートは3つあります。Cell(細胞) ポートは最も近い特徴点を指定する0〜1の数値を出力します。この値は、「細胞」内の、特徴点で定義されたすべての点と同じで、形が不均一で色も異なる細胞のパターンを作るのに便利です。Distance 1(距離1) ポートと Distance 2(距離2) ポートはそれぞれ、特徴点に最も近い距離と2番目に近い距離を出力します。どちらのパターンも、多様な手続きテクスチャを作るのに役立ちます。
このほかに便利なパターンは、減算モジュールで (Distance 2)-(Distance 1) を計算して得られます。この方法で、細胞間の境界が0に等しく、それぞれの細胞の中心に向かって増えていくパターンになります。
 |
 |
 |
 |
| Cell | Distance 1 | Distance 2 | (Distance 2)-(Distance 1) |
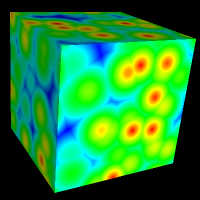
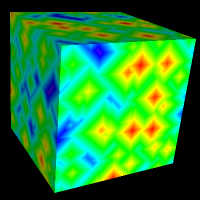
上記のすべての図で、最も近い特徴点は Euclidean Distance(ユークリッド距離)をもとにしています。細胞モジュールにはほかに2つの距離法 "City Block distance(市街地のブロック区切り距離)" と "Chess Board distance(チェス盤距離)" があります。それぞれの結果は特有のもので、異なるタイプのテクスチャを作るのに役立ちます。距離法を選ぶには、モジュールをダブルクリックします。以下の図の立方体の色は、細胞モジュールに3つの距離法のうちの1つを使った Distance 1 出力をもとにしています。
 |
 |
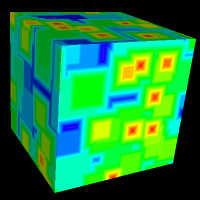 |
| Euclidean Distance | City Block Distance | Chess Board Distance |
| D = sqrt(dx*dx+dy*dy+dz*dz) | D = |dx|+|dy|+|dz| | D = max(|dy|, |dy|, |dz|) |
マーブル
大理石の筋模様を思わせるパターンを生成します。上述の乱流関数で乱したサイン関数で帯を作ります。
f(x,y,z) = sin(x+t(x,y,z))
パラメータで帯同士の間隔と、乱流関数の振幅とオクターブを設定します。Noise(ノイズ) 入力は乱流モジュールのノイズ入力に相当します。
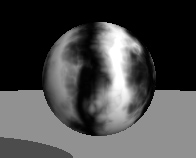
木目
木目のテクスチャを生成するのに便利です。与えられた点への出力は Y 軸からの距離に比例し、乱流関数が追加されます。"Only Output Fraction(出力の比率のみ)" オプションを選ぶと出力から余り1が取り払われ、出力は輪の幅にわたり0から1に増える同心円の集まりになります。
パラメータで輪の間隔と、乱流関数の振幅とオクターブ数を設定します。Noise(ノイズ) 入力は乱流モジュールのノイズ入力に相当します。
このモジュールの最も一般的な利用方法はグラデーション関数に出力を送ることで、これで色の帯の適切な連続が得られます。この方法を使うときは普通、"Only Output Fraction" オプションは 使わない のがベストです。代わりに色彩関数は周期的にします。そうしないと、木目関数のアンチエイリアスで見た目が人工的になってしまいます。

格子
長方形ごとの出力が0か1のチェッカーボードパターン(市松模様)を生成します。実際にこれは市松模様の3次元的な一般化です。これを積み上げた立方体と考えてください。この関数の値は隣り合った立方体同士で交互に異なります。

レンガ
レンガ模様を生成します。これはレンガ(出力=1)とレンガ同士の隙間(出力=0)でできています。レンガはレイヤー(層)状に積み上げられていて、各レイヤーの位置はその下のレイヤーとズレています。パラメータで、ブロックの高さ・レンガの間の隙間の幅・隣り合うレイヤー同士のズレを設定できます。
格子モジュールと同じく、これは3次元的なパターンです。X-Y 平面か Y-Z 平面で切ると、断面に標準的な 2D のレンガ模様が生じます。

画像
手続きの一部として画像ファイルが使えます(GIF か JPEG フォーマット)。出力ポートは4つで、一番上は色ポート(指定の点での画像の色を出力)です。ほかの3つは数値ポートで、それぞれ赤・緑・青を出力します(訳注: ver 2.9 では出力ポートは5つで、一番下は「マスク」です)。
モジュールをダブルクリックするとウインドウが現れ、そこで画像の選択と以下のパラメータの設定ができます。
- 画像のサイズ(X Size, Y Size)。デフォルト設定では大きな方の次元は1.0で、もうひとつの次元は、画像の形をもとに適正なアスペクト比が与えられます。
- 画像を X, Y 方向にタイル(Tile)並べするかどうか。このオプションを選ぶと、画像はその方向に無限に繰り返されます。選択しないと、(0, 0) の位置に画像のコピーが1枚だけ貼られ、その画像の外側の点への出力は0となります。
- X 方向/Y 方向に鏡反転(Mirror)するかどうか。このオプションを選んでタイル並べにすると、画像のコピーが、そのまま/反転 の互い違いに並びます。並んでいる画像同士の境目は、滑らかにブレンドされます。
前: 変換モジュール 次: プロバティウインドウ














